2D 상의 위성 궤도 모의하기

시간 경과에 따른 움직임은 다음 조건으로 궤도를 도는 위성에 대해 시뮬레이션됩니다.

주축의 근지점 반경 $r_p=9,600 \text{km}$

짧은 종단 반경 원점 반경 $r_a=21,000 \text{km}$

상수 $\mu=398,600$

궤도 운동에 대한 변수 계산

편심 $e$

$$e=\frac{r_a – r_p}{r_a + r_p} = 0.3725 $$

각운동량 $h$는 근지점 조건에서 계산됩니다.

$$h = \sqrt{r_p \mu \left(1 + e\right) }= 72,472 \text{km2/s}\leftarrow r=\frac{h^2}{\mu } \frac{1}{ 1 + e \text{cos}\theta}$$

궤도 주기 $T$

$$T=\frac{2 \pi}{\mu^2} \left( \frac{h}{\sqrt{1-e^2}} \right)^3 = 18,834 \text{초} = 5 .23 \text{시간}$$

시간 경과에 따른 변칙 계산

정의는 다음과 같습니다.

• $\theta$ : 진이상, 진이상
• $M_e$ : 중간이상, 중간이상
• $E$ : 괴상한 이상 현상

시간 참조로 인해 $t \rightarrow M_e \rightarrow E \rightarrow \theta$를 순서대로 계산해야 합니다.

평균 이상 $M_e$와 시간 $t$의 관계는 다음과 같다.

$$M_e = \frac{\mu^2}{h^3} \left(1-e^2 \right)^{3/2} t = \frac{2\pi}{T}t$$

평균 이상 $M_e$와 편심 이상 $E$의 관계는 다음과 같다.

이를 케플러 방정식이라고 합니다.

$$M_e = Ee\text{sin} E$$

편심 이상 $E$와 진 근점 이상 $\theta$의 관계는 다음과 같다.

$$\frac{E}{2} = \sqrt{\frac{1-e}{1+e}} \text{tan}\frac{\theta}{2}$$

$$\theta = 2 \text{tan}^{-1}\left( \sqrt{\frac{1+e}{1-e}} \text{tan} \frac{E}{2} \right )$$

진정한 근지점 이상에서 속성 계산

초점 거리 $r$
$$r= \frac{h^2}{\mu} \frac{1}{1+e \text{cos}\theta }$$

방사 속도 $v_r$

$$v_r = \frac{\mu}{h} e \text{sin}\theta$$

횡속도 $v_{\perp}$

$$v_r = \frac{\mu}{h} \left(1+ e \text{cos}\theta \right)$$

MATLAB에서의 구현

위의 배열에 따라 구현된 코드는 다음과 같다.

참고로 평균 이상과 실제 이상은 vpasolve()를 이용하여 계산하였다.

안타깝게도 Colorscript는 MATLAB을 지원하지 않습니다.

결과

코드를 실행한 결과는 다음과 같습니다.

두 사이클을 실행합니다.

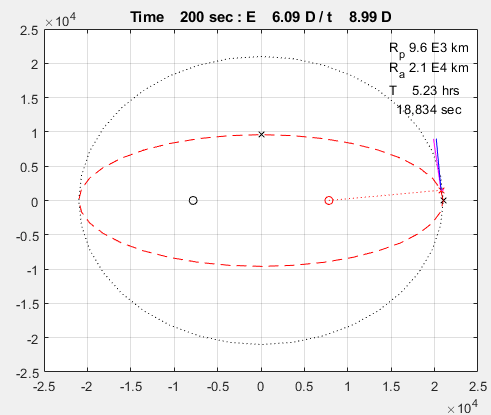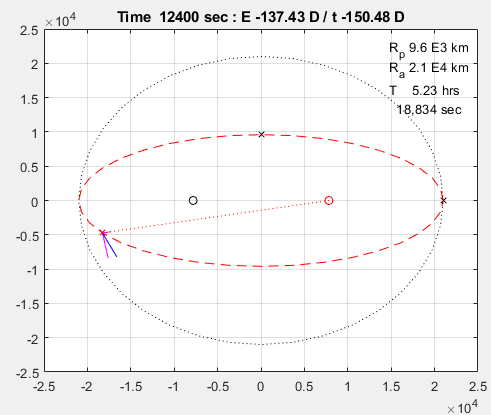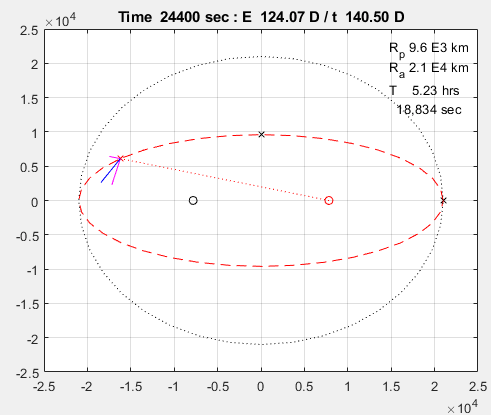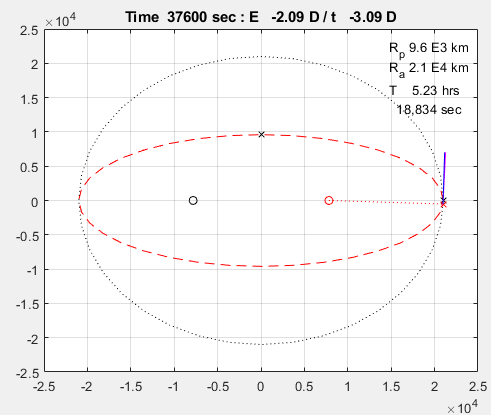
끝.